关于结构体中的内存分配
假设有如下结构体
struct Test
{
int Num;
int length;
int Width;
}test[1000];其中依次定义了 Num，Length，Width，均为 int，并 test[1000] 。
现在查看其内存地址
int* num = &test[0].Num;
cout << "Num " << &test[0].Num << " " << &test[1].Num << endl;
cout << "length " << &test[0].length << " " << &test[1].length << endl;
cout << "Width " << &test[0].Width << " " << &test[1].Width << endl;
cout << &num[0] << " " << &num[1] <<" " << &num[2] << " " << &num[3] << endl;输出如下
Num 00007FF7C8CDF180 00007FF7C8CDF18C
length 00007FF7C8CDF184 00007FF7C8CDF190
Width 00007FF7C8CDF188 00007FF7C8CDF194
00007FF7C8CDF180 00007FF7C8CDF184 00007FF7C8CDF188 00007FF6734FF18C可以看出如果将 num 指向了 &test[0].Num 即结构体的第一个变量，那么 num[0] 的地址就是 test[0].Num 的地址。
之后 num[1] 为下一个变量 int length 的地址，相差 4 个字节。
注意类型匹配，如果num为int类型，那么每一个函数地址均是 +4，即使结构体中有int之外的类型。
如果结构体中有double类型，那么如下
结构体
struct Rectangle
{
int Num;
double length;
double Width;
int test;
}rectangle[1000];输出
Num 00007FF74EA2F180 00007FF74EA2F1A0
length 00007FF74EA2F188 00007FF74EA2F1A8
Width 00007FF74EA2F190 00007FF74EA2F1B0
Test 00007FF74EA2F198 00007FF74EA2F1B8
00007FF74EA2F180 00007FF74EA2F184 00007FF74EA2F188 00007FF74EA2F18C可以看出，原本4字节大小的Num却使用了8字节空间
具体原因在:
数据结构对齐
如果将 double写在最前面可以解决，所以在定义变量的时候尽量将较大的数据写在前面。
结构体数组定义后不会立即分配内存
结构体排序去重
#include <stdio.h>
#include <iostream>
using namespace std;
struct Rectangle
{
int Num=0;
int length=0;
int Width=0;
}rectangle[1000];
void Input(int m) {
int tempOne, tempTwo;
for (int i = 0; i < m; i++)
{
cin >> rectangle[i].Num >> tempOne >> tempTwo;
if (tempOne > tempTwo)
{
rectangle[i].length = tempOne;
rectangle[i].Width = tempTwo;
}
else
{
rectangle[i].length = tempTwo;
rectangle[i].Width = tempOne;
}
}
}
void Resort(int m, int* num) //传入结构的第一个地址
{
for (int i = 0; i < m - 1; i++)
{
for (int j = 0; j < m - 1; j++) {
if (num[j*3]>num[(j+1)*3]) //共 3 个int
{
Rectangle Temp;
Temp = rectangle[j + 1];
rectangle[j + 1] = rectangle[j];
rectangle[j] = Temp;
}
}
}
}
void Output(int m) { //输出
for (int i = 0; i < m; i++)
{
cout << rectangle[i].Num << " " << rectangle[i].length << " " << rectangle[i].Width << endl;
}
}
void Handle(int m) {
Resort(m, &rectangle[0].Width); //先按照宽排序
Resort(m, &rectangle[0].length); // 按照长排序
Resort(m, &rectangle[0].Num); // 按照编号排序
}
int DelDup(int m) {
for (int i = 0; i < m-1; i++)
{
if (rectangle[i].Num == rectangle[i + 1].Num && rectangle[i].length == rectangle[i + 1].length && rectangle[i].Width == rectangle[i + 1].Width)
{
for (int j = i; j < m-1; j++)
{
rectangle[j] = rectangle[j + 1]; //复制后一位至前一位
}
m--; //减少数据量
i = i-1; //重新搜索重复值
}
}
return m;
}
int main() {
int n, m;
cin >> n;
while (n--) {
cin >> m;
Input(m);
Handle(m);
m = DelDup(m);
Output(m);
}
}关于malloc返回值
如图，因为需要存放malloc出的内存的长度，这就是为什么malloc需要传递长度参数，而对应的free函数却不需要传递长度参数的原因，因为内部以及保存长度啦，当free传递指针参数时，free会先去当前指针指向地址的前16字节获取长度后再释放内存。这里有个问题，64位机器存储长度只需要8个字节，这里却多了16个字节，另外8个字节起到什么作用呢？这里其实通过查看malloc源码的注释就可以看到：
/*
1056 malloc_chunk details:
1057
1058 (The following includes lightly edited explanations by Colin Plumb.)
1059
1060 Chunks of memory are maintained using a `boundary tag' method as
1061 described in e.g., Knuth or Standish. (See the paper by Paul
1062 Wilson ftp://ftp.cs.utexas.edu/pub/garbage/allocsrv.ps for a
1063 survey of such techniques.) Sizes of free chunks are stored both
1064 in the front of each chunk and at the end. This makes
1065 consolidating fragmented chunks into bigger chunks very fast. The
1066 size fields also hold bits representing whether chunks are free or
1067 in use.
1068
1069 An allocated chunk looks like this:
1070
1071
1072 chunk-> +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
1073 | Size of previous chunk, if unallocated (P clear) |
1074 +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
1075 | Size of chunk, in bytes |A|M|P|
1076 mem-> +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
1077 | User data starts here... .
1078 . .
1079 . (malloc_usable_size() bytes) .
1080 . |
1081 nextchunk-> +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
1082 | (size of chunk, but used for application data) |
1083 +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
1084 | Size of next chunk, in bytes |A|0|1|
1085 +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
1086
1087 Where "chunk" is the front of the chunk for the purpose of most of
1088 the malloc code, but "mem" is the pointer that is returned to the
1089 user. "Nextchunk" is the beginning of the next contiguous chunk.前8个字节表示之前的空间有多少没有被分配的字节大小，后8个字节表示当前malloc已经分配的字节大小。
函数指针
#include <stdio.h>
#define GET_MAX 0
#define GET_MIN 1
int get_max(int i,int j)
{
return i>j?i:j;
}
int get_min(int i,int j)
{
return i>j?j:i;
}
int compare(int i,int j,int flag)
{
int ret;
//这里定义了一个函数指针，就可以根据传入的flag，灵活地决定其是指向求大数或求小数的函数
//便于方便灵活地调用各类函数
int (*p)(int,int);
if(flag == GET_MAX)
p = get_max;
else
p = get_min;
ret = p(i,j);
return ret;
}
int main()
{
int i = 5,j = 10,ret;
ret = compare(i,j,GET_MAX);
printf("The MAX is %d\n",ret);
ret = compare(i,j,GET_MIN);
printf("The MIN is %d\n",ret);
return 0 ;
}int *f(int i, int j);
int (*p)(int i, int j);
前者是返回值是指针的函数；后者是一个指向函数的指针。
节点
s->next的意思是s指向的某个（如结构体）变量中的next这个成员本身
然后把p->next的地址赋值给s->next，也就是说s->next指向p->next
链表中使用的较多！一个链表的一个节点包括数据域和指针域两部分，s->next指向的是p->next这个节点！
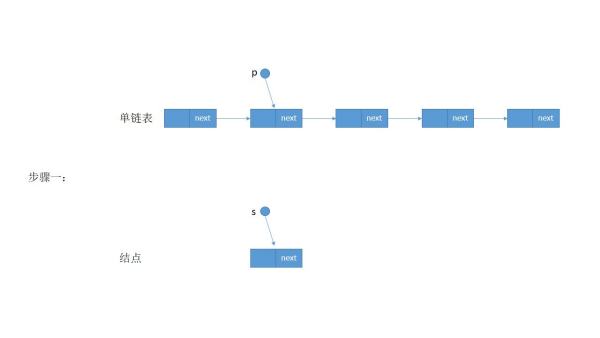
s->next = p->next; p->next= s;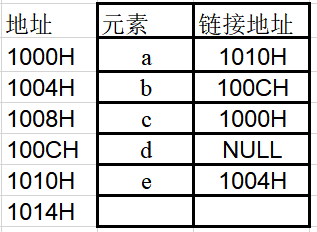
使用 typedef 为结构起别名
typedef 为这个新的结构起了一个别名，叫 Point，即：
typedef struct tagPoint Point因此，现在你就可以像 int 和 double 那样直接使用 Point 定义变量，如下面的代码所示：
Point oPoint1={100，100，0};Point oPoint2;定义结构体
typedef struct和struct的区别：
typedef struct tagMyStruct
{
int iNum;
long lLength;
} MyStruct;上面的tagMyStruct是标识符，MyStruct是变量类型（相当于（int,char等））。
这语句实际上完成两个操作：
- 定义一个新的结构类型
struct tagMyStruct
{
int iNum;
long lLength;
};分析：tagMyStruct称为“tag”，即“标签”，实际上是一个临时名字，不论是否有typedefstruct 关键字和tagMyStruct一起，构成了这个结构类型，这个结构都存在。
我们可以用struct tagMyStruct varName来定义变量，但要注意，使用tagMyStruct varName来定义变量是不对的，因为struct 和tagMyStruct合在一起才能表示一个结构类型。
- typedef为这个新的结构起了一个名字，叫MyStruct。
typedef struct tagMyStruct MyStruct;因此，MyStruct实际上相当于struct tagMyStruct，我们可以使用MyStruct varName来定义变量。 3.
typedef struct tagMyStruct
{
int iNum;
long lLength;
} MyStruct;在C中，这个申明后申请结构变量的方法有两种： （1）struct tagMyStruct 变量名 （2）MyStruct 变量名 在c++中可以有 （1）struct tagMyStruct 变量名 （2）MyStruct 变量名 （3）tagMyStruct 变量名
在C和C++里不同
在C中定义一个结构体类型要用typedef:
typedef struct Student
{
int a;
}Stu;于是在声明变量的时候就可：Stu stu1 如果没有 typedef 就必须用 struct Student stu1 来声明。
这里的 Stu 实际上就是 struct Student 的别名。Stu==struct Student
另外这里也可以不写Student（于是也不能 struct Student stu1 了，必须是 Stu stu1）
typedef struct
{
int a;
}Stu;但在c++里很简单，直接
struct Student
{
int a;
};于是就定义了结构体类型 Student，声明变量时直接 Student stu2；
在c++中如果用typedef的话，又会造成区别：
struct Student
{
int a;
}stu1;//stu1是一个变量
typedef struct Student2
{
int a;
}stu2;//stu2是一个结构体类型=struct Student使用时可以直接访问 stu1.a 但是 stu2 则必须先 stu2 s2 然后 s2.a=10
如果在c程序中我们写：
typedef struct
{
int num;
int age;
}aaa,bbb,ccc;这算什么呢？ 我个人观察编译器（VC6）的理解，这相当于
typedef struct
{
int num;
int age;
}aaa；
typedef aaa bbb;
typedef aaa ccc;也就是说 aaa,bbb,ccc 三者都是结构体类型。声明变量时用任何一个都可以,在c++中也是如此。但是你要注意的是这个在c++中如果写掉了typedef关键字，那么aaa，bbb，ccc将是截然不同的三个对象。
c语言结构体不能赋初始值
以前struct（包括类class，两者概念是差不多的）是杜绝在其体内直接给成员变量赋初始值的，但是 C++ 11可以给每个成员变量赋予默认的初始值，如下：
struct Student{
char* name = nullptr;
unsigned int age = 15;
int number = 21509111;
};如此一来，所有声明的新结构体对象就是默认上面的值。
C 语言中，「.」与「->」有什么区别？
结构体用点，结构体指针用箭头。
- 编译器会将
p->member变成访问p+offset_member这个内存地址的变量，p本身就是地址。 - 编译器会将
s.member变成访问&s+offset_member这个内存地址的变量，s并不是地址。
malloc
动态内存分配，此函数的返回值是分配区域的起始地址
新建一个节点的时候
LDataNode *s = (LDataNode *)malloc(sizeof(LDataNode));什么时候用？每个节点都需要 ->next,最好写个函数之类的
p->next = (LDataNode *)malloc(sizeof(LDataNode));
p = p->next;判断是否含有某数字或被其整除
while (num)
{
if (num % 10 == 7)
{
flag = 1;
break;
}
num /= 10;
}创建一个链表
#include <stdio.h>
#include <malloc.h>
typedef struct LinkDataNode
{ //数据节点
int data; //数据域
struct LinkDataNode *next; //下一个节点
} LDataNode;
typedef struct LinkHeadNode
{ //头节点
int count; //总共节点数
LDataNode *next; //下一个节点
LDataNode *tail; //最后一个节点
} LHeadNode;
int main()
{
LHeadNode *phead = NULL;
phead = (LHeadNode *)malloc(sizeof(LHeadNode));
if (phead == NULL)
{
printf("内存分配失败");
return -1;
}
scanf("%d", &phead->count);
return 0;
}判断队列已满
假设一个循环队列 Q[Maxsize]
队头指针为 front
队尾指针为 rear
队列的最大容量为 MaxSize
判断该队的列满条件是: front==(rear+1) % MaxSize
%MaxSize 是消除绕圈，然后rear的下一个是front即满
此时队列的有效长度是： (rear+maxSize-front) % maxSize
其中有一个空
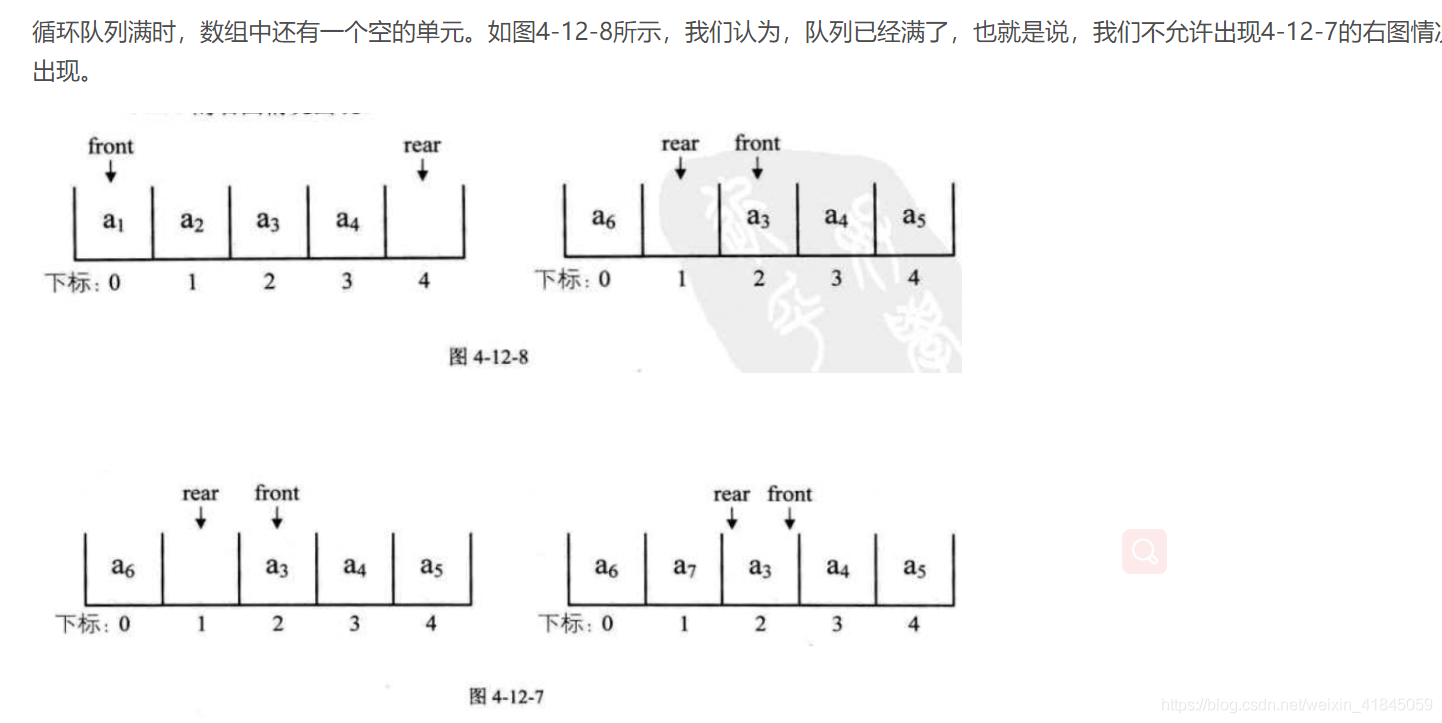
少用一个元素的空间。约定入队前，测试尾指针在循环意义下加1后是否等于头指针，若相等则认为队满（注意：rear所指的单元始终为空）；
例：若用一个大小为6的数组来实现循环队列，且当前rear和front的值分别为5和1，则当前队列的元素个数是（ 4 ）
因为rear虽然有编号，但并不存元素
数组操作
指针的移动
那么如何使指针变量指向一维数组中的其他元素呢？比如，如何使指针变量指向 a[3] 呢？
同样可以写成 p=&a[3]。但是除了这种方法之外，C 语言规定：如果指针变量 p 已经指向一维数组的第一个元素，那么 p+1 就表示指向该数组的第二个元素。
注意，p+1 不是指向下一个地址，而是指向下一个元素。“下一个地址”和“下一个元素”是不同的。比如 int 型数组中每个元素都占 4 字节，每字节都有一个地址，所以 int 型数组中每个元素都有 4 个地址。如果指针变量 p 指向该数组的首地址，那么“下一个地址”表示的是第一个元素的第二个地址，即 p 往后移一个地址。而“下一个元素”表示 p 往后移 4 个地址，即第二个元素的首地址。
指针运算符（& 和 *）
取地址运算符 &
& 运算符读作**"取地址运算符"，这意味着，&var** 读作"var 的地址"。
间接寻址运算符 *
间接寻址运算符 ，它是 & 运算符的补充。 是一元运算符，返回操作数所指定地址的变量的值。
栈与队列与链表
区别
队列
队列 是一种数据结构，其特点是先进先出，后进后出，只能在队首操作（比如删除、读取等），在队尾增加。 队列的存储方式 既可以使用 线性表 进行存储，也可以使用 链表 进行存储。
栈
栈 是一种数据结构 ，只能在 一端 进行操作，如插入和删除等操作 ，按照先进后出 （FILO）的原则存储数据。
链表
链表 ，是一种数据的存储方式（与其对应的是 顺序存储 结构），存储的数据在内存中 不连续的 ，用 指针 对数据进行访问。
操作
队列先进先出，栈先进后出。 栈是限定只能在表的一端进行插入和删除操作的线性表。 队列是限定只能在表的一端进行插入和在另一端进行删除操作的线性表。
遍历数据速度不同。
栈只能从头部取数据，也就最先放入的需要遍历整个栈最后才能取出来，而且在遍历数据的时候还得为数据开辟临时空间，保持数据在遍历前的一致性。
队列则不同，它基于地址指针进行遍历，而且可以从头或尾部开始遍历，但不能同时遍历，无需开辟临时空间，因为在遍历的过程中不影像数据结构，速度要快的多
顺序储存与链式存储
优缺点
① 顺序存储时，相邻数据元素的存放地址也相邻（逻辑与物理统一）；要求内存中可用存储单元的地址必须是连续的。
优点：存储密度大（＝1），存储空间利用率高。缺点：插入或删除元素时不方便。
②链式存储时，相邻数据元素可随意存放，但所占存储空间分两部分，一部分存放结点值，另一部分存放表示结点间关系的指针
优点：插入或删除元素时很方便，使用灵活。缺点：存储密度小（<1），存储空间利用率低。
使用情况
顺序表适宜于做查找这样的静态操作；链表宜于做插入、删除这样的动态操作。
若线性表的长度变化不大，且其主要操作是查找，则采用顺序表；
若线性表的长度变化较大，且其主要操作是插入、删除操作，则采用链表。
比较
顺序表与链表的比较，基于空间的比较，存储分配的方式
顺序表的存储空间是静态分配的，链表的存储空间是动态分配的
存储密度 = 结点数据本身所占的存储量/结点结构所占的存储总量
顺序表的存储密度 = 1
链表的存储密度 < 1
基于时间的比较，存取方式
顺序表可以随机存取，也可以顺序存取，链表是顺序存取的
插入/删除时移动元素个数
顺序表平均需要移动近一半元素，链表不需要移动元素，只需要修改指针
栈模板（顺序结构）
#include <stdio.h>
#include <malloc.h>
typedef int SElemType;
typedef struct {
SElemType* base; //地址用int表示
SElemType* top; //地址用int表示
int stacksize; //空间大小
}SqStack;
//构造一个空栈
int InitStack(SqStack* S) {
S->base = (SElemType*)malloc(100 * sizeof(SElemType)); //暂时分配100个int空间
if (!S->base)
return -1;
S->top = S->base;
S->stacksize = 100;
return 0;
}
//入栈
int Push(SqStack* S, SElemType e) {
if ((S->top - S->base) >= S->stacksize) {
S->base = (SElemType*)realloc(S->base, (S->stacksize + 10) * sizeof(SElemType)); //每次加10个int空间
if (!S->base)
return -1;
S->top = S->base + S->stacksize;
S->stacksize += 10;
}
*(S->top) = e; //寻址，将S->top指向的地址的值赋值为e
S->top++; //S->top指向下一个地址
return 0;
}
//判断是否为空栈
int StackEmpty(SqStack* S) {
if (S->top == S->base)
return 1;
else
return 0;
}
//出栈，用e返回S的顶元素
void Pop(SqStack* S, SElemType* e) {
if (S->top == S->base)
return;
*e = *(S->top - 1); //寻址，将S->top-1指向的地址的值赋值给e,因为最后一个top始终为空，等待输入数据
S->top--; //S->top指向上一个地址
}
//清理栈
void ClearStack(SqStack* S) {
S->top = S->base;
}
//摧毁栈
void DestroyStack(SqStack* S) {
free(S->base);
S->base = NULL;
S->top = NULL;
S->stacksize = 0;
}
int main()
{
SqStack* M = NULL;
M = (SqStack*)malloc(sizeof(SqStack));
return 0;
}链表模板（链结构）
#include <stdio.h>
#include <malloc.h>
typedef struct LinkDataNode
{ //数据节点
int data; //数据域
struct LinkDataNode *next; //下一个节点
} LDataNode;
typedef struct LinkHeadNode
{ //头节点
int count; //总共节点数
LDataNode *next; //下一个节点
LDataNode *tail; //最后一个节点
} LHeadNode;
int OutputNode(LHeadNode *phead) //输出
{
LDataNode *p = phead->next;
while (phead->count--)
{
printf("%d\n", p->data);
p = p->next;
}
return 0;
}
LDataNode *InitNode() //为节点分配内存
{
LDataNode *p = (LDataNode *)malloc(sizeof(LDataNode));
if (p == NULL)
{
printf("内存分配失败");
return NULL;
}
p->next = NULL;
return p;
}
int main()
{
LHeadNode *phead = NULL;
phead = (LHeadNode *)malloc(sizeof(LHeadNode));
if (phead == NULL)
{
printf("内存分配失败");
return -1;
}
scanf("%d", &phead->count);
return 0;
}队列模板（链结构）
#include <stdio.h>
#include <malloc.h>
typedef struct LinkDataNode
{ //数据节点
int data; //数据域
struct LinkDataNode* next; //下一个节点
} LDataNode;
typedef struct LinkHeadNode
{ //头节点
int count; //总共节点数
LDataNode* front; //头
LDataNode* rear; //尾
} LHeadNode;
LDataNode* InitNode() //为节点分配内存
{
LDataNode* p = (LDataNode*)malloc(sizeof(LDataNode));
if (p == NULL)
{
printf("内存分配失败");
return NULL;
}
p->next = NULL;
return p;
}
void InputNode(LHeadNode* HeadNode)
{
LDataNode* pnode = InitNode();
HeadNode->front = pnode;
for (int i = 1; i <= HeadNode->count; i++)
{
HeadNode->rear = pnode;
pnode->data = i;
LDataNode* pnew = InitNode();
pnode->next = pnew;
pnode = pnew;
}
HeadNode->rear->next = HeadNode->front;
}
int OutputNode(LHeadNode* Mhead,int n) //输出
{
LDataNode* Mp = Mhead->front;
while (n--)
{
printf("%d %d\n", Mp->data);
Mp = Mp->next;
}
return 0;
}
int main()
{
int i = 0;
LHeadNode* Mhead = NULL;
Mhead = (LHeadNode*)malloc(sizeof(LHeadNode));
if (Mhead == NULL)
{
printf("内存分配失败");
return -1;
}
InputNode(Mhead);
OutputNode(Mhead, Nhead, i);
return 0;
}树
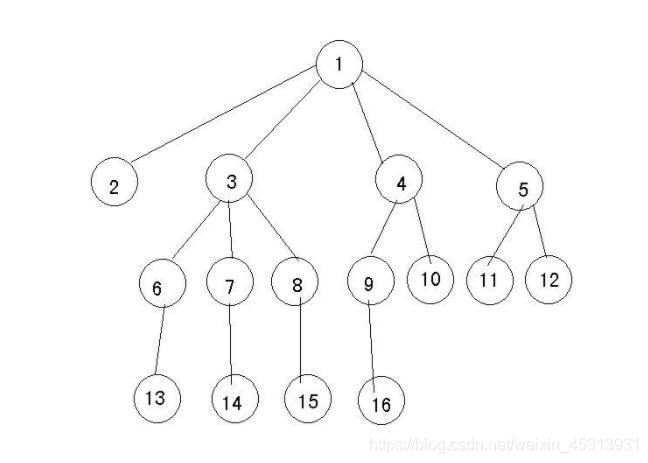结点拥有的子树个数称为结点的度，比如结点①的度为4，结点②的度为0，结点③的度为3。
对于树而言，树的度为树内各结点最大的度，从图中可知，结点①的度是最大的，为4，所以这棵树的度为4。
叶子结点是离散数学中的概念。 一棵树当中没有子结点（即度为0）的结点称为叶子结点，简称“叶子”。 叶子是指出度为0的结点，又称为终端结点
例：首先定义二叉树的度为子节点的个数，因此根据这个概念，节点情况只有0，1，2三种情况，分别用n0,n1,n2表示。 一个棵树的节点总数=n0+n1+n2 如图：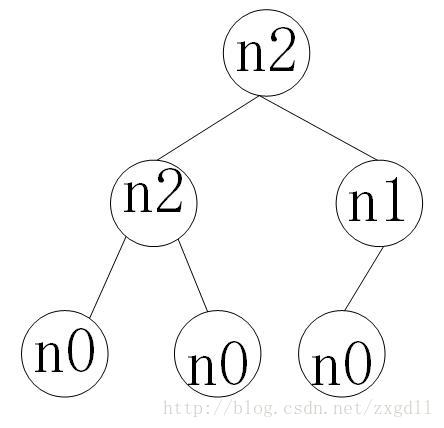 
当节点数N为奇数时，说明该树结构中没有度为1的节点。 当节点数为偶数时，说明有一个度为1的节点，如上图情况。 对于一个非空二叉树，有以下等式成立 n0=n2+1
举例说明： 1.设一棵完全二叉树共有699个节点，则在该二叉树中的叶节点数是什么？ n=n0+n1+n2 n0=n2+1 n=699，奇数，说明n1为0； n=n0+n0-1 n0=350，所以叶节点数为350。
- 一棵度为3的树中，有3度的结点100个，有2度的结点200个，有叶子结点多少个？
还是和上面一样的解题过程，我稍微简略一点写，思路都是一样的
n = n0 + n1 + n2 + n3
e = n - 1 = n0 + n1 + n2 + n3 - 1 //边数为节点总数量和-1
e = n0 * 0 + n1 * 1 + n2 * 2 + n3 * 3 //边数为各度节点的数量*度数相加
n0 + n1 + n2 + n3 - 1 = n0 * 0 + n1 * 1 + n2 * 2 + n3 * 3
n0 = n2 + n3 * 2 + 1
则叶子结点的个数为401个
·总结为：各节点数量的和-1=各节点的数量*度数相加
满二叉树和完全二叉树的区别
满二叉树
对于满二叉树，除最后一层无任何子节点外，每一层上的所有结点都有两个子结点二叉树。
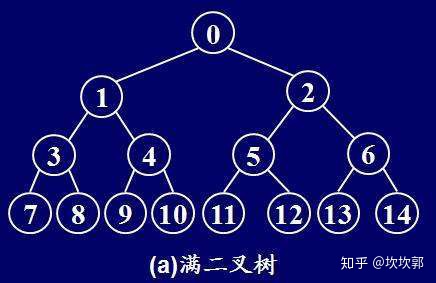
定义：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是(2^k) -1 ，则它就是满二叉树。
完全二叉树
完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
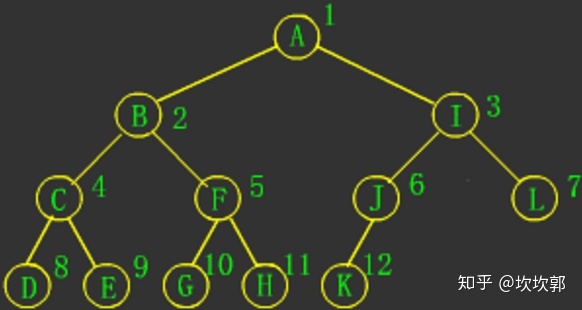
定义：若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。（如果总节点数为奇数则每一个都是两个子节点，偶数的话必定有一个是n1）
·总结
若一棵完全二叉树有768个结点,则该二叉树中叶子结点的个数是（384）
n0 + n1 + n2-1 =n0 * 0 + n1 * 1 + n2 * 2，化简得 n0 - 1 = n2
n0 + n1 + n2 = 768，根据性质节点总数为偶数，则n1 = 1，得n0 + n2 = 767
得n0=384
二叉树节点遍历
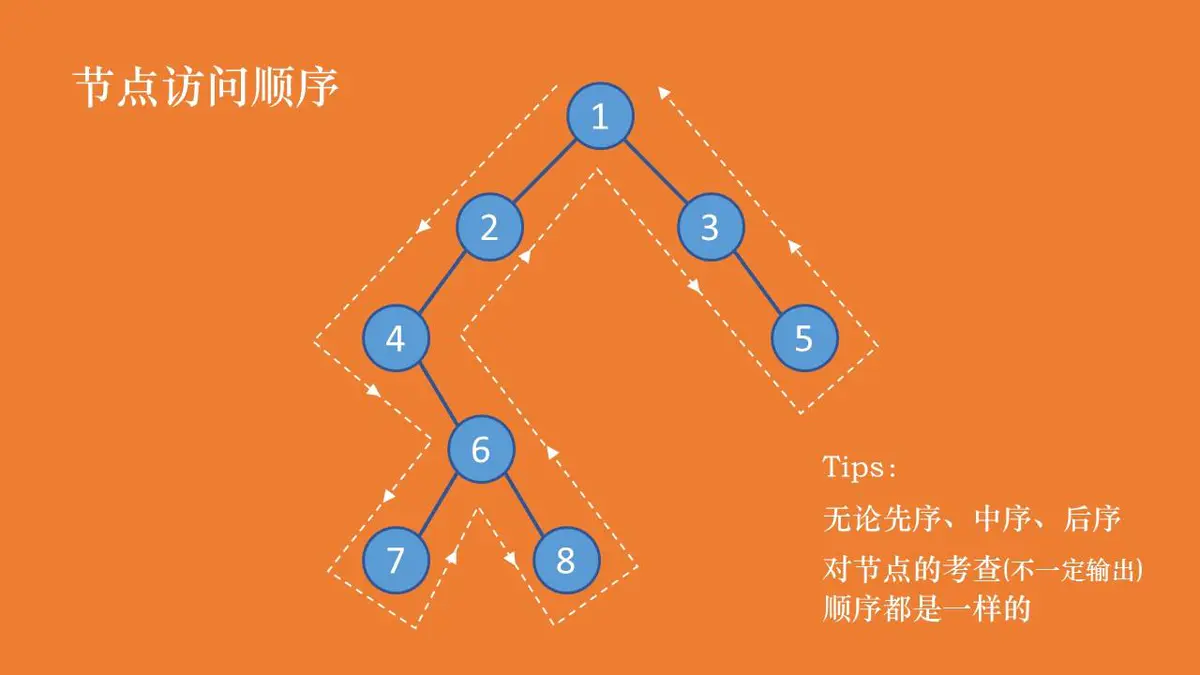
先序：1 2 4 6 7 8 3 5 中序：4 7 6 8 2 1 3 5 后序：7 8 6 4 2 5 3 1
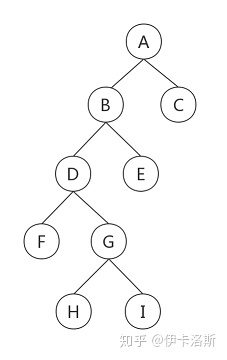
前序遍历A-B-D-F-G-H-I-E-C 前序(根左右)
中序遍历F-D-H-G-I-B-E-A-C 中序(左根右)
后序遍历F-H-I-G-D-E-B-C-A 后序(左右根)
遍历推树
序列化二叉树的一种方法是使用前序遍历。当我们遇到一个非空节点时，我们可以记录下这个节点的值。如果它是一个空节点，我们可以使用一个标记值记录，例如
#。
_9_
/ \
3 2
/ \ / \
4 1 # 6
/ \ / \ / \
# # # # # #例如，上面的二叉树可以被序列化为字符串 "9,3,4,#,#,1,#,#,2,#,6,#,#"，其中 # 代表一个空节点。
代码
遍历的时候传递指针值即可，但在生成的时候需要&引用
比如
void PreOrderTraverse(BiTNode* &T) { //前序遍历
NodeData ch;
ch = getchar();
if (ch == '\n') {
return;
}else{
if (ch == '^') {
T = NULL;
}
else {
T = (BiTNode*)malloc(sizeof(BiTNode));
T->weight = ch;
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
}
}以上代码是生成前序遍历树，如果直接传递进去指针值的话
BiTNode* ROOT=NULL;
PreOrderTraverse(ROOT);
void PreOrderTraverse(BiTNode* T) { //前序遍历生成
NodeData ch;
ch = getchar();
if (ch == '\n') {
return;
}else{
if (ch == '^') {
T = NULL;
}
else {
T = (BiTNode*)malloc(sizeof(BiTNode));
T->weight = ch;
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
}
}
void PreOrderTraverses(BiTNode* T) { //前序遍历
if (T == NULL) {
return;
}
PrintfElem(T);
PreOrderTraverses(T->lchild);
PreOrderTraverses(T->rchild);
}此时，传入函数的ROOT的地址值为0，函数接收到的值也是0，这时对T执行malloc函数，假设T值被赋值为1000。
那么下面递归 PreOrderTraverse(T->lchild); 调用的是1000->lchild，然后依次都是在1000之后赋值。
那再回到主函数，ROOT的值仍然是0，因为从始至终都没有对ROOT的值进行操作，在PreOrderTraverse函数中都是对malloc后的ROOT进行的操作即对1000进行操作，与原值没有关系。在之后再调用遍历函数传递ROOT值的时候就会发生NULL的情况了。
这时候如果修改函数接收值为BiTNode* &T即引用类型，那对T的操作就是对ROOT的操作，函数中的T值被malloc那么主函数也会相应的改变。
模板
#include <stdio.h>
#include <malloc.h>
typedef char NodeData;
typedef struct {
NodeData weight; //储存数据
BiTNode* parent; //双亲指针
BiTNode* lchild; //左孩子指针
BiTNode* rchild; //右孩子指针
}BiTNode;
void PrintfElem(BiTNode* Node) {
printf("%c", Node->weight);
}
void InOrderTraverse(BiTNode* T) { //中序遍历
if (T == NULL) {
return;
}
InOrderTraverse(T->lchild);
PrintfElem(T);
InOrderTraverse(T->rchild);
}
void PreOrderTraverse(BiTNode* T) { //前序遍历
if (T == NULL) {
return;
}
PrintfElem(T);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
void PostOrderTraverse(BiTNode* T) { //后续遍历
if (T == NULL) {
return;
}
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
PrintfElem(T);
}
void PreOrderTraverse(BiTNode* &T) { //前序遍历生成
NodeData ch;
ch = getchar();
if (ch == '\n') {
return;
}else{
if (ch == '^') {
T = NULL;
}
else {
T = (BiTNode*)malloc(sizeof(BiTNode));
T->weight = ch;
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
}
}
int main()
{
BiTNode* ROOT=NULL;
PreOrderTraverse(ROOT);
InOrderTraverse(ROOT);
printf("\n");
PostOrderTraverse(ROOT);
return 0;
}哈德曼树构建
有数据WG={7，19，2，6，32，3，21，10}，则所建Huffman树的树高是（ ），带权路径长度WPL为（）
接下来记住一个原则，那就是找当前树的根结点和剩余叶子结点的最小的两个值，然后组成新的树杈。
首先，从19、6、7、3、32、10、21、2 中选择频数最小的两个叶子结点，分别为2和3，计算两个结点的和5作为根：
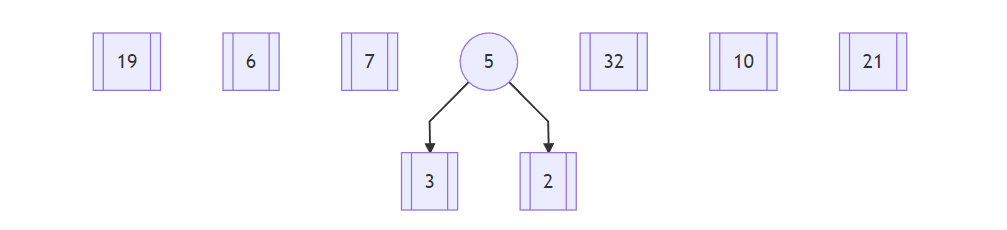
接着，从19、6、7、5、32、10、21 中选择两个最小的结点，分别是根结点5和叶子结点6，计算两个结点的和11作为新的树根：
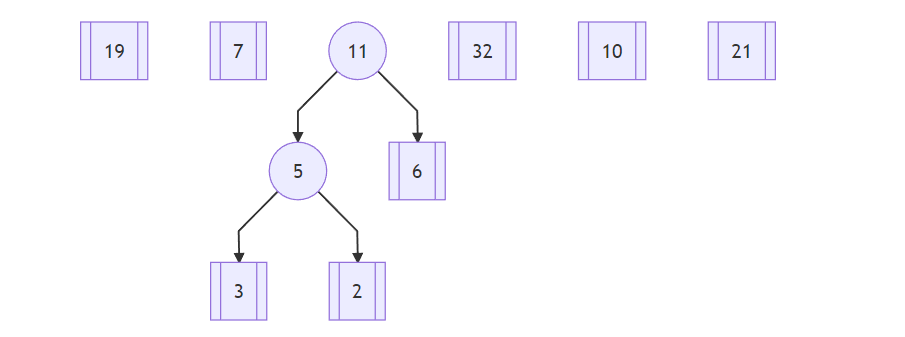
然后，从19、7、11、32、10、21 中选择两个最小的结点，这次都是叶子结点，分别为7和10，计算两个结点的和17形成一颗新的树：
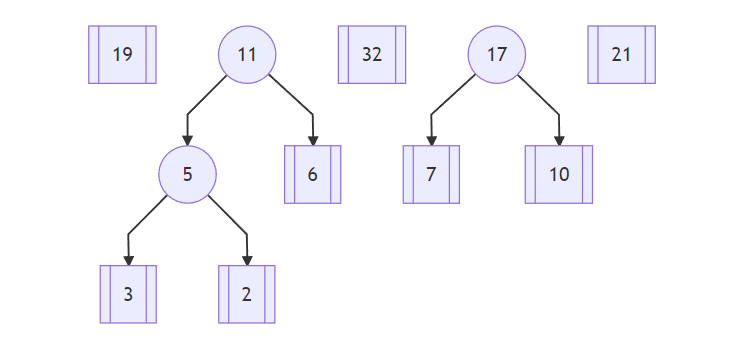
继续，从 19、11、32、17、21 中选择最小的 11 和 17 这两个树的根结点，计算两个结点的和 28 作为组合树的根结点：
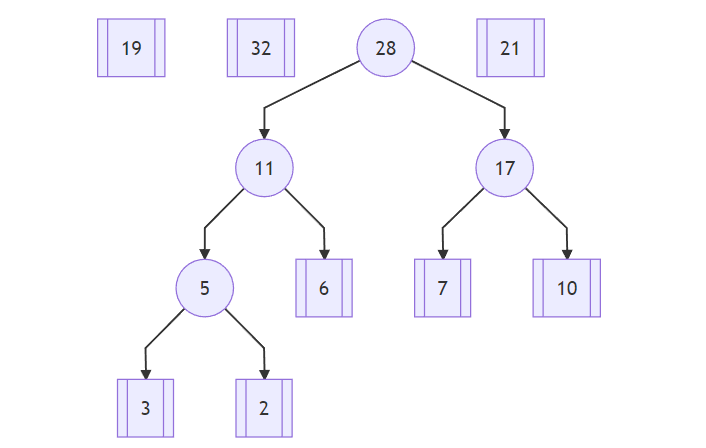
然后，从 19、32、28、21 中选择最小的 19 和 21 这两个叶子结点，计算两个结点的和 40 形成一棵新的树：
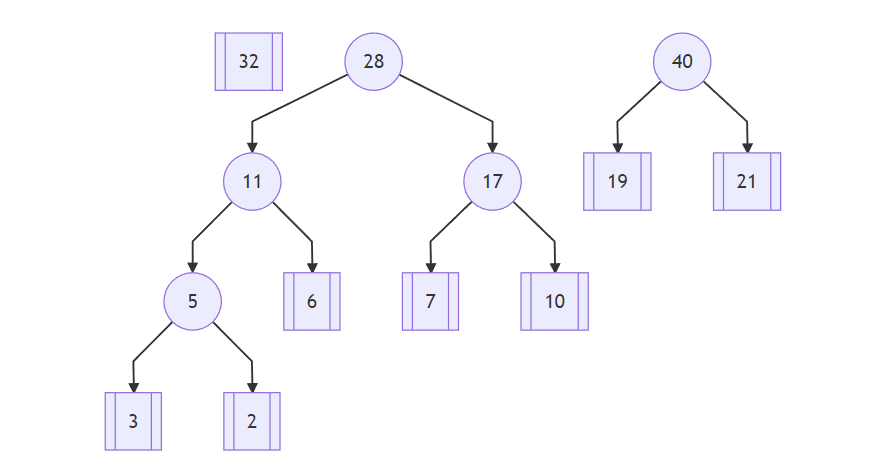
接下来，从 32、28、 40 中选择最小的 32 和 28 这两个结点，求和 60 构成一棵树，根结点为60：
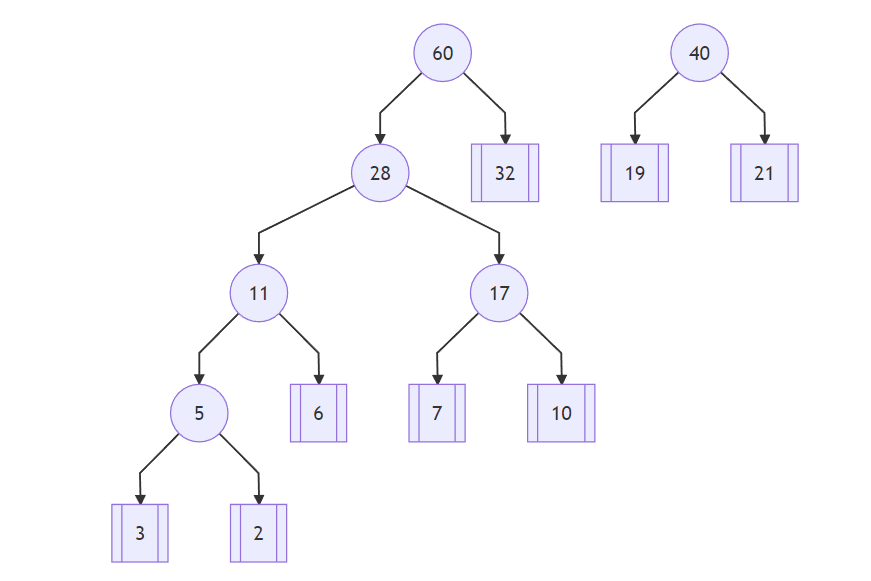
最后把剩下的 40 和 60 两个结点连在一起，和为100就得到了一颗哈夫曼树：
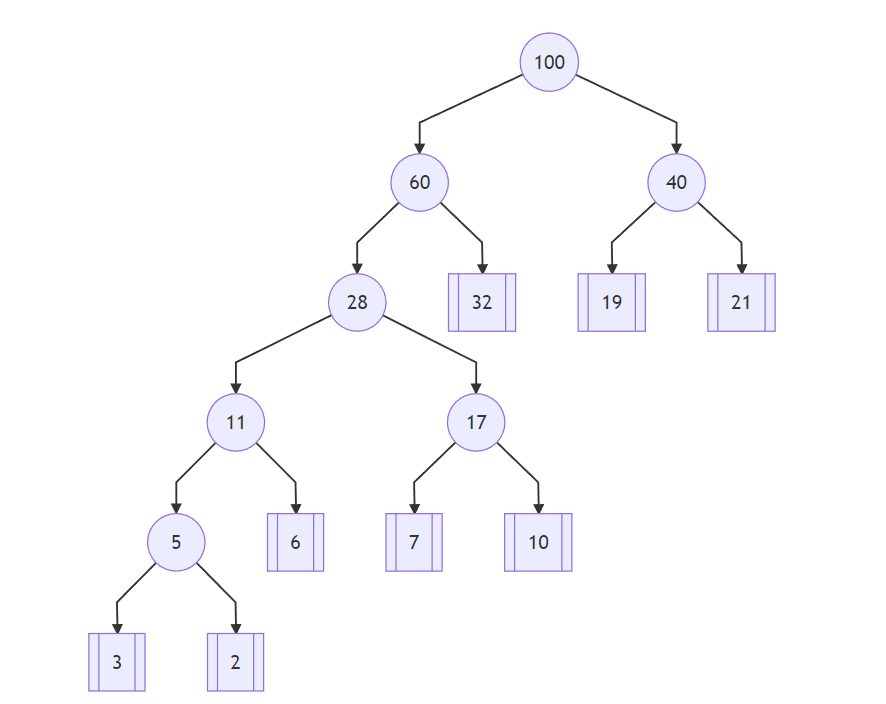
按照上面的定义来算，这颗二叉树的带权路径长度为：
WPL = 2 * (32 + 19 + 21) + 4 * (6 + 7 + 10) + 5 * (3 + 2) = 261
其实还有另一种计算带权路径长度的方法，那就是把除根结点以外的所有数字都加起来：
WPL = 60 + 40 + 28 + 32 + 19 + 21 + 11 + 17 + 5 + 6 + 7 + 10 + 3 + 2 = 261
编码
我们用统计数量的字母来替换频数，然后在树的左右指针上分别标上数字就可以得到：
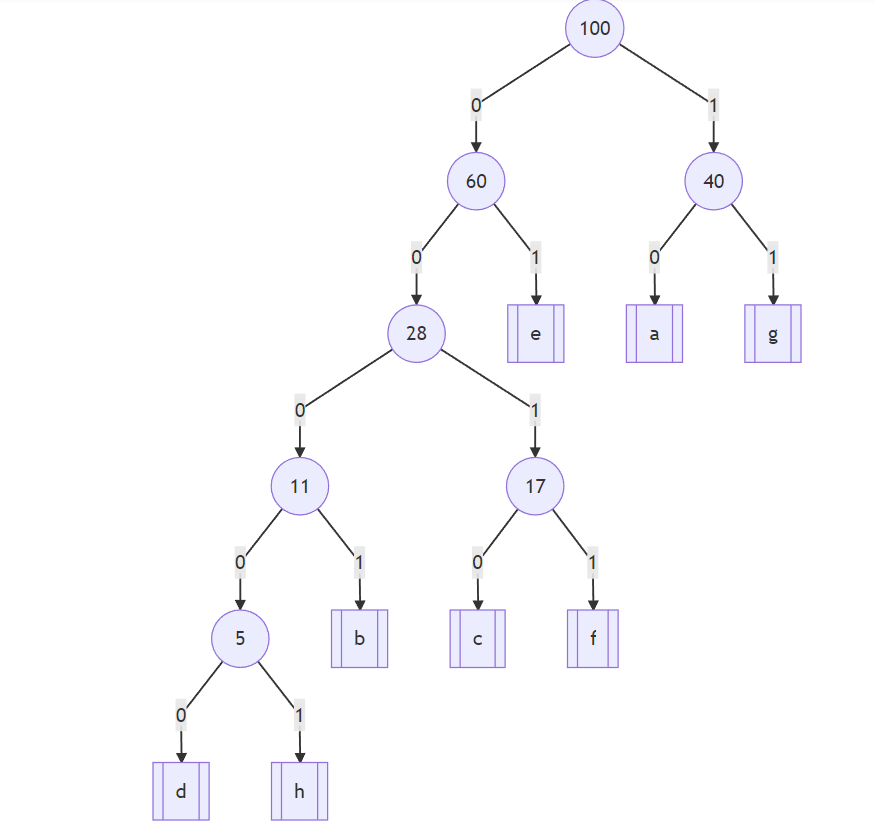
至此我们就可以给出编码了呀，从根结点走到每个叶子结点路径上经过的0和1就是编码内容，编码表如下：
a–>10 b–>0001 c–>0010 d–>00000 e–>01 f–>0011 g–>11 h–>00001
要想等长编码这8个字母最少需要4个bit，采用哈夫曼编码以后最少用2bit，最多用5bit，这是考虑了出现频率以后的结果，在传输大量数据的时候，采用哈夫曼编码会是一个更优的解决方案。
二叉树不唯一
总结
- 树的带权路径长度是指树的所有叶子结点的带权路径长度之和，简称WPL
- 当使用已知结点作为叶子结点，用其构造的所有树中，带全路径长度最小的树被称为最优二叉树，也就是哈夫曼树
- 哈夫曼树可以用来编码，采用哈夫曼编码后的信息可以可以使空间利用更加高效
- 哈夫曼树的构造并不是唯一的，相同的权值结点完全可以构造出不同形态的哈夫曼树，甚至连高度都不同
- 哈夫曼编码还保证了长编码不与短编码冲突的的特点
1.为什么要保证长编码不与短编码冲突？
冲突情况：如果我们已经确定D，E，F，G 用 01 ，010 ，10，001的2进制编码来传输了。那么想传送FED时，我需要传送 1001001，接收方可以把它解析为FDG（10 01 001），当然也能解析为FED（10 010 01），他两编码一样的，这就是编码冲突，（这里编码冲突的原因，也是因为编码时，D的编码是E的编码的左起子串了）显然这是不行的，就像我说压脉带，你如果是日本人会理解为 （你懂得），这就是发出同一种语，得出不同的意的情况。所以不能让一个字母的二进制代表数，为另一个字母的二进制代表数的子串。但为什么实际情况只要求编码时，一个编码不是另一编码的****左起子串呢而不是绝对意义上的*非子串*呢，因为计算机从数字串的左边开始读，如果从右边读，那么可以要求是非右起（无奈）。你又可以问了为什么编码要求是非左起或非右起**不直接规定不能是子串呢（也行，不过=>），比如说原文中B就是C，F，G的子串，那这不就不符合规则了么。这里是为了哈夫曼的根本目的，优化编码位占用问题，如果完全不能有任何子串那么编码将会非常庞大。但这里计算机是一位一位的·读取编码的，只需要保证计算机在读取中不会误判就行。并且编码占用最少。
code：011**0101001**110
左起子串：011
右起子串：110
绝对非子串：*1110111 此串在code中完全找不到*
2.那么哈夫曼树怎么避免左起子串问题呢？
因为哈夫曼是从叶子节点开始构造，构造到根节点的，而且构造时，都是计算两个权值的节点的和再与其他叶子节点再生成一个父节点来组成一个新的树。并且不允许任何带有权值的节点作为他们的父节点。这也保证了所有带有权值的节点都被构造为了叶子节点。然后最后编码的时候是从根节点开始走到叶子节点而得出的编码。在有权值的节点又不会出现在任何一条路的路途中的情况，只会出现在终点的情况下，因此不会出现01代表一个字母011又代表一个字母。
又如原文ABC编码为10010011的情况，当计算机读到10时，由于有左起子串不冲突的原则。那么计算机完全可以保证当前的10就是A字母，然后再往下读010011的部分，然后当读到01时，也完全能确定B，C同理，而不用说因为会出现冲突的编码而接着继续读取之后的编码来确定前面的编码。这样对信息的判断和效率是相当的不利的，也不是说不可以。即使你ABCD,分别用01,011,0111,01111来代替也行，传输后也能精确识别，但是数据量极大呢，想代替整个中文编码呢，那0后面得多少个1才能代表完。因此哈夫曼就是为了获得最少编码量代替最多字符串，并且不冲突，系统不会误判而产生的。
3.这里要提一下同权不同构
已经有朋友问起这个问题了。这里要说一下哈夫曼树的构造并不是唯一的。
考虑如下情况：
有权值分别为 5,29,7,8,14,23,3,11的情况，可以如下图一样构造。
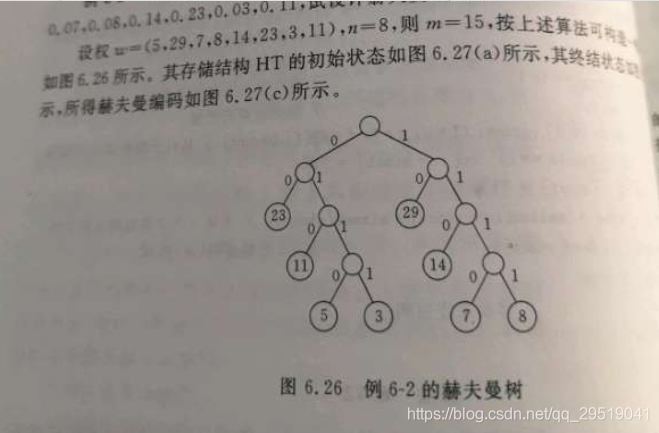
带权路径长度：
(5+3+7+8)*4+
(11+14)*3+
(23+29)*2
=271
也可以如下图构造：
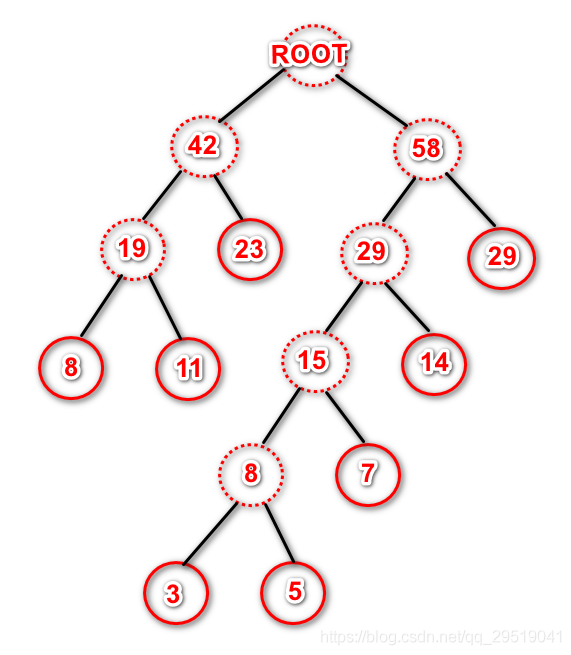
带权路径长度：（3+5)5+74+(8+11+14)*3+(23+29)*2=271
这两种不同的方式构造出来的哈夫曼树，得出的带权路径长度相等，那么选哪颗树都可以，这就叫同权不同构。
7
ABC^^^^
ABC^^^^
ABC^^^^
ABC^^^^
ABC^^^^
ABC^^^^
ABC^^^^图
1.具有4个顶点的无向完全图有（）条边。
[解析]有n(n-1)/2条边的无向图称为完全图，即6条。
强连通图的边问题
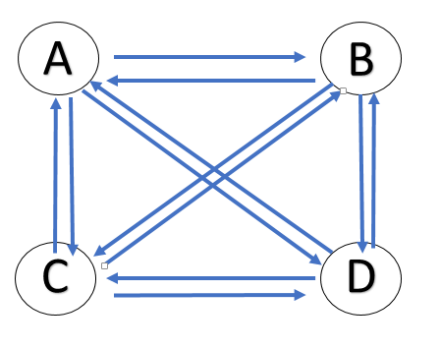
有n个顶点的强连通图最多有n（n-1）条边，最少有n条边。
（1）最多的情况：即n个顶点中两两相连，若不计方向，n个点两两相连有n（n-1）/2条边，而由于强连通图是有向图，故每条边有两个方向，n（n-1）/2×2=n（n-1），故有n个顶点的强连通图最多有n（n-1）条边。
（2）最少的情况：即n个顶点围成一个圈，且圈上各边方向一致，即均为顺时针或者逆时针，此时有n条边。
图的深度优先遍历类似于二叉树的
深度优先遍历是先序遍历，广度优先遍历是层次遍历(以距离起点的路径长度为层次进行扩展先被访问的顶点的邻接点，也先被访问)
最小生成树
Kruskal算法
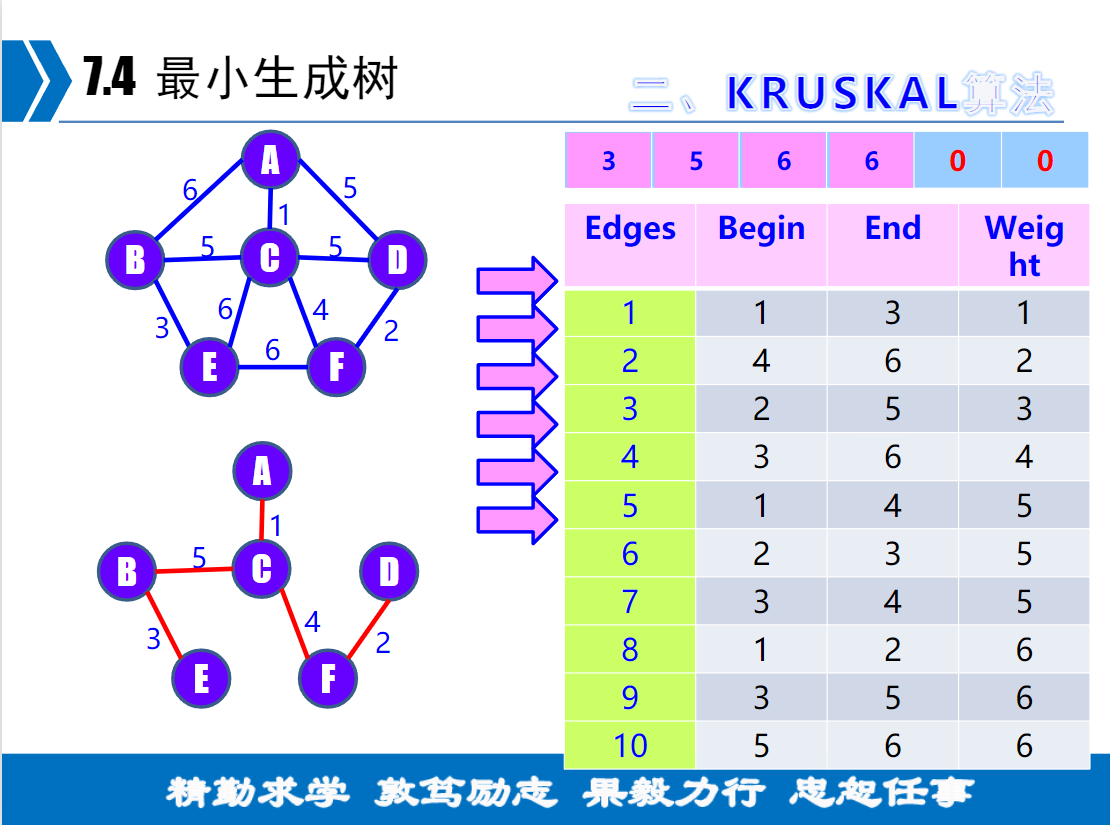
1.定义结构 先按照节点值从小到大排序，然后再按照权值从小到大排序
typedef struct Edge
{
int Begin；
int End；
int Weight；
} Edge；
Edge edge[G.numArcs]2.定义一个所有节点数大小的数组在节点值的位置记录他下一个节点的位置
3.从第一个节点开始，在num[begin]的位置记录end，如果不为空则递归到num[num[begin]],如果这个值与end相等则构成回环，忽略。
int Find ( int *circle , int f ) //判断循环回路
{
while( circle[ f ] > 0) f = circle[ f ]；
return f；
}直到全部节点记录完。
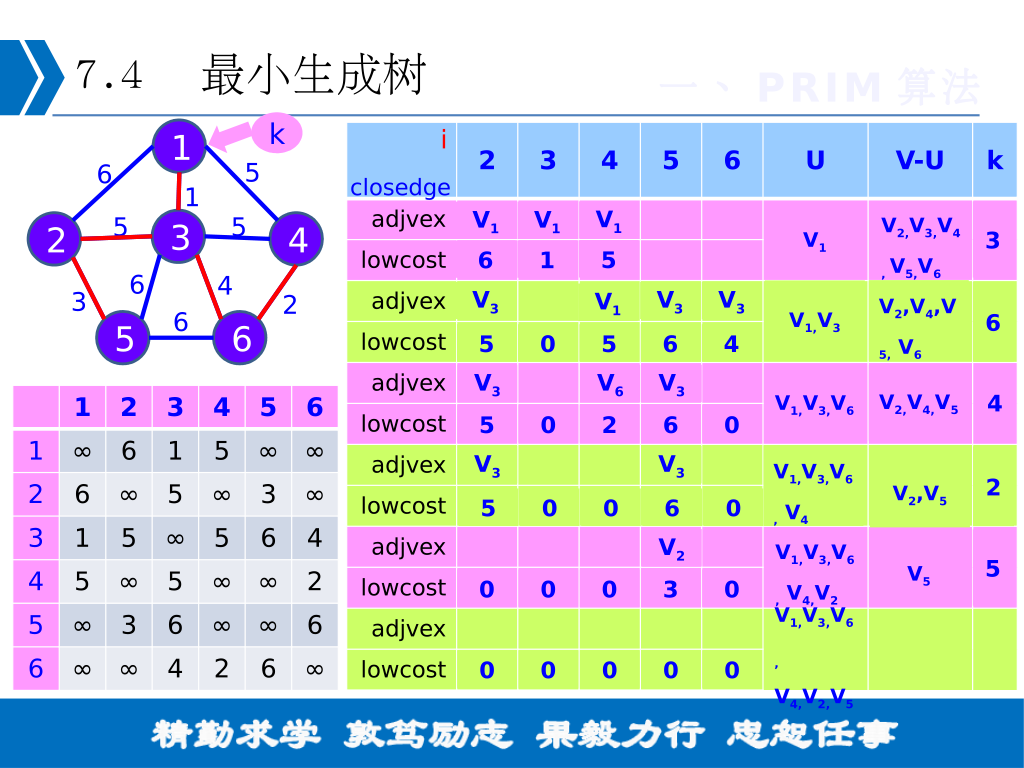
普里姆算法查找最小生成树的过程，采用了贪心算法的思想。对于包含 N 个顶点的连通网，普里姆算法每次从连通网中找出一个权值最小的边，这样的操作重复 N-1 次，由 N-1 条权值最小的边组成的生成树就是最小生成树。
那么，如何找出 N-1 条权值最小的边呢？普里姆算法的实现思路是：
- 将连通网中的所有顶点分为两类（假设为 A 类和 B 类）。初始状态下，所有顶点位于 B 类；
- 选择任意一个顶点，将其从 B 类移动到 A 类；
- 从 B 类的所有顶点出发，找出一条连接着 A 类中的某个顶点且权值最小的边，将此边连接着的 A 类中的顶点移动到 B 类；
- 重复执行第 3 步，直至 B 类中的所有顶点全部移动到 A 类，恰好可以找到 N-1 条边。
折半查找ASL
例：给11个数据元素有序表（2,3,10,15,20,25,28,29,30,35,40）采用折半查找。则ASL成功和不成功分别是多少？
首先画出判定树，
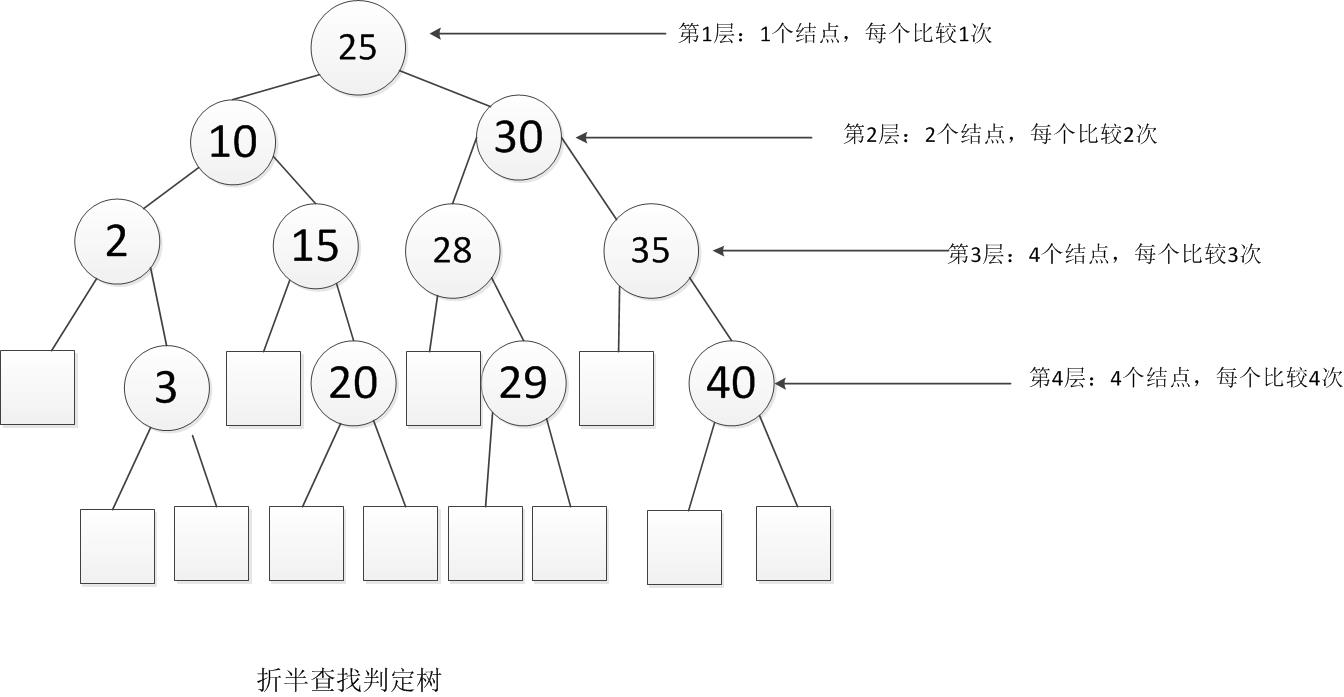查找成功时总会找到途中某个内部结点，所以成功时的平均查找长度为
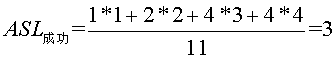即25查找一次，成功，10,30要查找2次，成功，2,15,28,35要查找3次，成功，3,20,29,40要查找4次，成功。 而不成功的平均查找长度为 
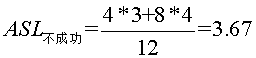，为什么这么算呢，因为内部结点都能查找成功，而查找不成功的就是那些空的外部结点，所以到查询到2的左孩子，15的左孩子，28的左孩子，35的左孩子，3的左右孩子，20的左右孩子，29的左右孩子，40的左右孩子时，都是查找不成功的时候。如我要找1，比25小，转向左子树，比较一次，比10小，转左子树，2次，比2 小，转左子树，3次，此时2无左子树，所以失败。所以
。
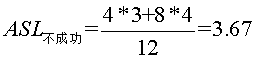散列表查找失败的平均查找长度
举个栗子：8个数字 key%11 如下算好了：
| 散列地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 关键字 | 33 | 1 | 13 | 12 | 34 | 38 | 27 | 22 | |||
| 冲突次数 | 0 | 0 | 0 | 2 | 3 | 0 | 1 | 7 |
什么叫做查找失败？比如你要查55这个关键字，你必须%11，等于0，查地址0为33，不对，下一位1，不对，继续往下查找直到出现空的才知道这个关键字一定不存在，否则就放在空着的那个地址。所以以上表，计算地址为0的关键字查了9次才才知道没有这个关键字称为查找失败；计算地址为1的关键字只有探测完1-8号才能确定该元素不存在，以此类推。但是注意了，如果计算地址为8的或者9的、10的，只需要查找一次就知道该地址为空，失败了。因此查找一次就行。而且要知道如果查找成功是除以关键字个数，但是查找失败是除以你要模的数字本题是11，千万记住了，不是地址个数，不是关键字个数。综上所述，查找失败的平均查找长度为（9+8+7+6+5+4+3+2+1+1+1）/11=47/11。放心错不了，书上原题。
还要注意，如下题型H(key)=key%7：
| 散列地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 关键字 | 98 | 22 | 30 | 87 | 11 | 40 | 6 | 20 |
千万注意，%7只能映射到0-6，散列函数不可能映射7，因此查找失败平均查找长度为（9+8+7+6+5+4+3)/7=6。看到这你可能想骂娘，啥玩意儿，别急。我会让你看懂，因为我最讨厌虾鸡吧写博客的傻逼玩意儿，写的不清楚又不解释，还误人子弟，low咖！！！好了回归正题。首先要知道，我们求平均查找长度其实在求概率，对于成功的平均查找长度，查找每个元素的概率是1/8，这个8就是关键字个数。就是说，查找成功你只能选择8个中的一个，否则成功不了，所以都是在等概率1/8情况下。查找失败也是一样，这里对每个位置的查找概率都是1/7,注意7是你要模的数字，就是说，你随便拿几个数，模7，只能是0、1、2、3、4、5、6，其中一种情况，不可能是7、8以后的数字，所以只需要计算地址在0-6中的概率。如果计算地址后为0，那么需要比较9次，以此类推，所以只能是上面的计算式子，别搞错了噢！还有要注意有些散列表不是完全填满，中间有空位，那相信你看完上面原理就不用我解释了，找到了空位还没有就说明不存在嘛，否则它就占位这个空位了。注意以上所讨论的全部是线性探测，如果是平方探测注意左右跳动，具体问题具体分析，就不展开了。
在递归中使用++需要注意
需要区分i++和++i的区别
例如：
a = ++i，相当于 i=i+1; a = i;
a = i++，相当于 a = i; i=i+1;
比如下面的代码
void test(int i)
{
printf("%d",i);
test(++i);
}
test(1);如果使用的是i++的话相当于传入的值是test（1）；然后i再自加，这样无论循环多少次都是test（1）
如果使用的是++i的话相当于传入的是i=i+1，这样每循环一次i都会增加。
引申
参数计算顺序
先执行哪个参数和参数的计算顺序有关，而c/c++中没有规定函数参数的计算顺序，这个和编译器有关，代码参数的计算顺序决定了实际输出。
#include <stdio.h>
int main () {
int a = 2;
printf("%d, %d, %d", a, (a = (a + 2)), (a = (a + 3)));
system("pause");
return 0;
}
//win10 + VS2019 输出: 7, 7, 7
//clang输出结果 2 4 7vs的计算顺序是从右至左，clang的计算顺序是从左至右，具体的计算流程分析就很简单了。
对于c/c++函数参数的读取顺序，参数入栈时顺序从右向左入栈，但是在入栈前会先把参数列表里的表达式从右向左算一遍得到表达式的结果，最后再把这些运算结果统一入栈。
在参数入栈前，编译器会先把参数的表达式都处理掉，对于一般的操作来说，参数入栈时取值是直接从变量的内存地址里取的，但是对于a++操作，编译器会开辟一个缓冲区来保存当前a的值，然后再对a继续操作，最后参数入栈时的取值是从缓冲区取，而不是直接从a的内存地址里取。
结论
因为函数参数的计算顺序依照编译器的实现，所以在编码中避免编写诸如 fun(++x, x+y)这种的程序，其在不同的平台得到的结果可能不一样，但是在面试中可能遇到这样的问题，所以我们需要知其然更要知所以然。
二分搜索
int search(int a[], int x, int low, int high) //二分搜索
{
if (low >= high)
{
return -1;
}
else
{
int mid = (low + high) / 2;
if (x == a[mid]) //查找到就返回下标
{
return mid;
}
if (x < a[mid]) //待查找的数小于中间的数，就在左半部分查找
{
return search(a, x, low, mid - 1);
}
else
{
return search(a, x, mid + 1, high);
}
}
}题目 抓住那头牛
【题意】
约翰希望立即抓住逃亡的牛。当前约翰在节点N ，牛在节点K （0≤N , K ≤100 000）时，他们在同一条线上。约翰有两种交通方式：步行和乘车。如果牛不知道有人在追赶自己，原地不动，那么约翰需要多长时间才能抓住牛？
- 步行：约翰可以在一分钟内从任意节点X 移动到节点X -1或X+1。
- 乘车：约翰可以在一分钟内从任意节点X 移动到节点2×X 。
【输入输出】
输入：
两个整数N 和K 。
输出：
单行输出约翰抓住牛所需的最短时间（以分钟为单位）。
【样例】
提示： 在输入样例中抓住牛的最快方法是沿着路径5-10-9-18-17前进，需要4分钟。
【思路分析】
可以采用深度优先搜索和广度优先搜索两种方法解决。
【算法设计】
① 深度优先搜索方法
根据输入样例，约翰在5的位置，牛在17的位置。约翰可以先乘车到10，步行退回到9，然后乘车到18，步行退回到17，抓到牛，一共4步。
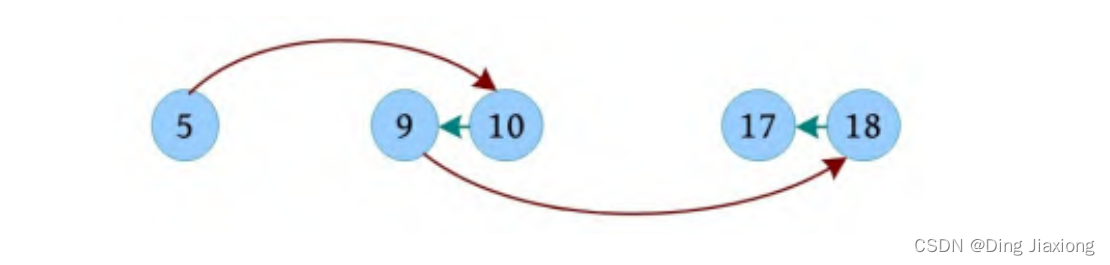假设约翰和牛的位置分别为n 和k ，则求解步骤如下：
- 如果n =0，则先走1步到1，n =1，否则无法乘车，因为0的两倍还是0。
- 进行深度优先搜索，dfs(t )表示求解约翰从初始位置n 到达位置t 的最小步数。
- 如果t ≤n ，因为不可以向后乘车，只能一步一步地后退，则需要n -t 步。
- 如果t 为偶数，则比较从t/2 向前乘车到t、 从n 一步一步向前走到t ，采用哪种方案使得步数最少，取最小值。第1种方案的步数为从初始位置到达t/2 的步数dfs(t /2)加上1次乘车所需步数，第2种方案的步数为t -n 。
- 如果t 为奇数，则比较从t -1向前1步到t （步数为dfs(t-1)+1）、从t +1向后1步到t （步数为dfs(t +1)+1），采用哪种方案使得步数最少，取最小值。
int dfs(int t){
if(t <= n){
return n - t;
}
if(t % 2 == 1){
return min(dfs(t + 1) + 1, dfs(t - 1) + 1);
}
else{
return min(dfs(t / 2) + 1, t - n);
}
}② 广度优先搜索算法
- 如果k ≤n ，因为不可以向后乘车，只能一步一步地后退，则需要n -k 步，否则执行步骤2。
- 从当前节点出发进行广度优先搜索，每个节点都可以扩展3个位置，判断该位置是否为牛的位置，如果是，则返回走过的步数；否则，判断位置是否有效（未超界且未访问），如果是，则将步数加1，并将位置入队。
- 如果队列不空，则一直进行广度优先搜索，直到找到牛的位置。
【完美图解】
从约翰的位置5出发进行广度优先搜索，节点5先扩展3个位置，然后节点6、4、10扩展，如下图所示。
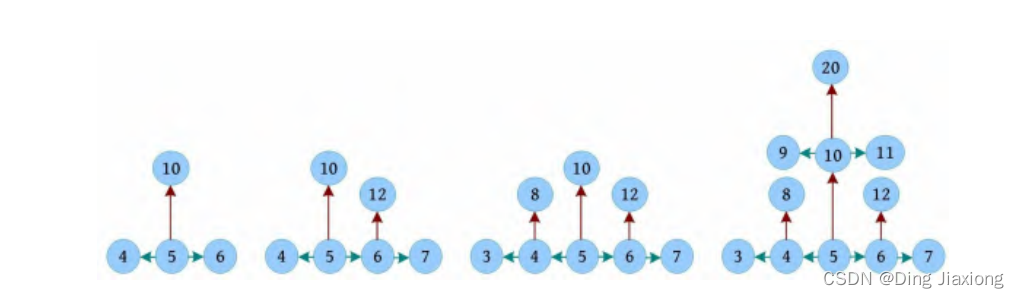
继续进行广度优先搜索，直到找到牛的位置，返回走过的距离。
从以上扩展可以看出，有很多无效搜索，效率比采用深度优先搜索要低。因为在一条直线上，所以采用深度优先搜索效果更好；如果在二维地图上，则采用广度优先搜索效果更好。
【算法实现】
#include<iostream>
#include<algorithm>
using namespace std;
int n , k;
int dfs(int t){
if(t <= n){
return n - t;
}
if(t % 2){
return min(dfs(t + 1) + 1 , dfs(t - 1) + 1);
}
else{
return min(dfs(t / 2) + 1 , t - n);
}
}
int main(){
while(cin >> n >> k){
int ans = 0;
if(n == 0){ //特判
n = 1;
ans = 1;
}
ans += dfs(k);
cout << ans << endl;
}
return 0;
}