我的笔记本

E

e 与复利息息相关。复利是指在一定时间内，本金每经过一个确定的时间间隔所产生的利息，而复利计算中的自然常数 e 的出现与复利息息相关。

假设一笔本金 P ，以年利率 r 进行复利，每年复利次数为 n 次，则在一年后，本金 P 的总收益为：

P * (1 + r/n)^n

当 n 趋近于无穷大时，上式的极限值就是 e^(r)P，其中 e 是自然常数。因此，e 可以用来表示复利的极限情况，即当复利次数趋近于无穷大时，本金的增长速度会趋近于 e^(r) 倍。

简单的线性回归

要构建一个通过身高预测体重的线性回归模型，你需要做以下步骤：

收集数据集并进行清理，将身高和体重之间的对应关系记录下来，一般说，数据集可以从公共数据仓库中获取，例如UCI Machine Learning Repository。
将数据集分成训练集和测试集。一般来说，我们将数据集的 70% 分配给训练集，将剩下的 30% 分配给测试集。
导入相关的 Python 库，例如 NumPy、Pandas 和 Matplotlib。
为模型选择最优的算法，例如梯度下降法或正规方程法。
初始化模型参数并根据算法进行训练。
使用测试集测试模型预测的精确度，例如使用平均绝对误差（Mean Absolute Error）或平均平方误差的（Mean Squared Error）来度量。

下面是一个用 Python 构建简单线性回归模型的例子：

python

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression

# 从文件中读取数据集
data = pd.read_csv('heights_weights.csv')

# 将数据集分为训练集和测试集
train_data = data.sample(frac=0.7, random_state=42)
test_data = data.drop(train_data.index)

# 初始化模型
reg_model = LinearRegression()

# 训练模型
reg_model.fit(train_data[['Height']], train_data['Weight'])

# 在测试集上进行预测
predictions = reg_model.predict(test_data[['Height']])

# 计算预测精确度
mse = np.mean((predictions - test_data['Weight']) ** 2)
mae = np.mean(abs(predictions - test_data['Weight']))
rmse = np.sqrt(mse)

print("Mean Squared Error:", mse)
print("Mean Absolute Error:", mae)
print("Root Mean Squared Error:", rmse)

在上面的代码中，使用了 Pandas 从 CSV 文件中加载了一个数据集，并对训练集和测试集进行了分割。我们使用了 Scikit-learn 的线性回归模型，将身高作为自变量，体重作为因变量进行建模。我们使用训练集对模型进行了训练，并使用测试集对模型进行了测试，并计算了平均绝对误差、平均平方误差和平均平方根误差等指标来评估模型预测的精度。

分析

这两个数组中的数据似乎是身高和体重之间的关系数据。可以使用 NumPy 库提供的数组运算功能来进行简单线性回归分析，从而估计身高和体重之间的线性关系。

以下是一个简单的示例代码，使用 scikit-learn 库的线性回归模型来实现：

python

import numpy as np
from sklearn.linear_model import LinearRegression

TrainDataHeight = np.array([0.86, 0.96, 1.12, 1.35, 1.55, 1.63, 1.71, 1.85])
TrainDataWeight = np.array([12, 15, 20, 35, 48, 51, 59, 75])

# 构建线性回归模型
model = LinearRegression()
model.fit(TrainDataHeight.reshape(-1, 1), TrainDataWeight)

# 打印模型参数
print('Intercept: ', model.intercept_)
print('Coefficient: ', model.coef_)

# 预测新数据
height_new = 1.6
weight_new = model.predict([[height_new]])
print('Predicted weight for height {}: '.format(height_new), weight_new[0])

上述代码中，首先定义了 TrainDataHeight 和 TrainDataWeight 两个数组，分别表示身高和体重的数据。然后，使用 LinearRegression 类来构建线性回归模型，并使用 fit 方法来拟合数据。

接着，使用 intercept_ 和 coef_ 属性分别获取模型的截距和系数。最后，使用 predict 方法来预测新的数据。

请注意，在实际应用中，需要对数据进行更多的处理和分析，以确保模型的准确性和可靠性。同时，也需要对模型进行评估和优化，以进一步提高模型的性能和泛化能力。

.reshape 有什么作用

.reshape() 是 NumPy 数组对象的一个方法，用于调整数组的形状（维度）。它可以改变数组的维数，也可以改变各维度的大小，但是数组的总元素数量不能改变。

.reshape() 方法可以传递一个元组（tuple）作为参数，其中每个元素表示新维度的大小。如果元组中的元素个数与原数组的维度数不同，则需要在元组中相应位置上传递 -1，表示该维度的大小由系统自动推断。

在机器学习中，常常需要将输入数据调整成指定的维度，以输入到模型中进行训练或预测。例如，在上一个问题的示例代码中，使用 .reshape(-1, 1) 将 TrainDataHeight 数组从一维转换为二维，以满足 LinearRegression() 类的输入要求。

以下是一个简单的示例代码，用于演示 .reshape() 方法的用法：

python

import numpy as np

# 创建一个 2x3 的数组
arr = np.array([[1, 2, 3], [4, 5, 6]])
print(arr)

# 将数组转换为 3x2 的形状
arr_reshaped = arr.reshape((3, 2))
print(arr_reshaped)

# 将数组转换为 1x6 的形状（使用 -1 自动推断维度大小）
arr_reshaped = arr.reshape((-1,))
print(arr_reshaped)

上述代码中，首先创建了一个 2x3 的数组 arr，然后使用 .reshape() 方法将其转换为 3x2 和 1x6 的形状，并输出结果。

请注意，在使用 .reshape() 方法时，需要确保新维度的大小与原数组的总元素数量相同，否则会引发 ValueError 异常。此外，还需要注意数组的存储顺序（行优先或列优先）可能会影响 .reshape() 方法的结果。

为什么TrainDataHeight 需要Reshape,而TrainDataWeight不用

在机器学习中，通常要求输入数据的格式为二维数组，其中一维表示样本数量，另一维表示每个样本的特征数量。在本问题中，TrainDataHeight 和 TrainDataWeight 分别表示身高和体重的数据，需要将它们转换为二维数组的形式，以便于输入到模型中进行训练或预测。

但是，TrainDataHeight 和 TrainDataWeight 的含义不同，因此需要采用不同的转换方式。

对于 TrainDataWeight 数组，它只包含一个特征（体重），因此可以看做是一个一维数组，可以直接作为模型的输入。在模型训练时，LinearRegression() 类会自动将其转换为二维数组的形式，其中一维表示样本数量，另一维表示特征数量（这里为 1）。

对于 TrainDataHeight 数组，它也只包含一个特征（身高），但是它是一个一维数组，不能直接作为模型的输入。因此，需要使用 .reshape() 方法将其转换为二维数组的形式，其中一维表示样本数量，另一维表示特征数量（这里为 1）。

因此，TrainDataHeight 需要使用 .reshape() 方法转换为二维数组的形式，而 TrainDataWeight 不需要进行转换，可以直接作为模型的输入。

中文画图乱码

http://c.biancheng.net/matplotlib/9284.html

重写配置文件

通过临时重写配置文件的方法，可以解决 Matplotlib 显示中文乱码的问题，代码如下所示：

matlab

import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题

数据归一化

python

from sklearn.preprocessing import MinMaxScaler

# 数据归一化
scaler = MinMaxScaler() # 实例化模型
X_train_normalized = scaler.fit_transform(x_train) # 训练缩放
X_test_normalized = scaler.transform(x_test) # 测试数据缩放

meshgrid

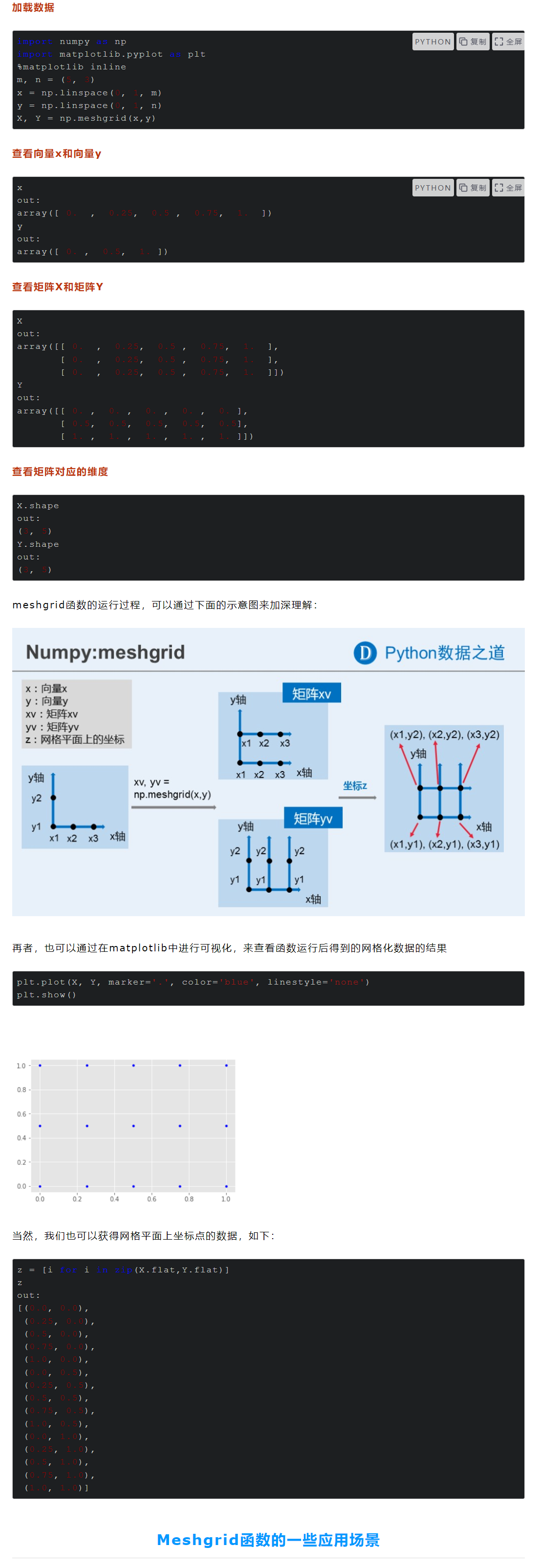
假设有一个一维数组 x 和一个一维数组 y，它们分别是：

python

import numpy as np

x = np.array([1, 2, 3])
y = np.array([4, 5])

我们可以使用 meshgrid 生成网格点坐标矩阵：

(x为横向，y为竖向，以确保每个都有对应组合成不同值，x与y结合成格子)

python

X, Y = np.meshgrid(x, y)
print(X)
print(Y)

输出结果为：

[[1 2 3]
 [1 2 3]]
[[4 4 4]
 [5 5 5]]

可以看到，X 的第一行和第二行都是原始数组 x 的复制，而 Y 的第一列和第二列都是原始数组 y 的复制。

重塑数组结构

reshape(-1, 1) 是 NumPy 中用于改变数组形状的方法之一，它的作用是将一个一维数组转化为二维数组，其中第一个维度是 -1，意思是让 NumPy 自动计算该维度的大小，第二个维度为 1，表示每个元素只有一个特征。

举个例子，假设有一个一维数组 a，它包含 6 个元素，我们可以使用 reshape(-1, 1) 将其转化为一个 6 行 1 列的二维数组 b：

python

import numpy as np

a = np.array([1, 2, 3, 4, 5, 6])
b = a.reshape(-1, 1)

print(b)
# 输出：
# [[1]
#  [2]
#  [3]
#  [4]
#  [5]
#  [6]]

这个方法也可以用于将一个多维数组转化为一维数组，例如 a.reshape(-1) 将一个二维数组展平成一维数组。

损失函数选择

nn.CrossEntropyLoss() 是一个用于计算交叉熵损失的函数，通常用于多分类问题中。

nn.MSELoss() 是一个用于计算均方误差损失的函数。它可以用于回归问题中，衡量模型的预测值与真实值之间的差距。

应用

自动编码解码器

自动编码解码器使用 MSELoss 均方误差损失函数。

MSE 损失函数假设输入和重构之间的关系是线性的。

在自动编码器中，我们希望解码器的输出尽可能接近原始输入，因此我们需要定义一个度量来衡量重构的质量。均方误差损失函数是衡量重构误差的一种常见选择。

MSE损失函数计算输入和目标之间的平均平方差，它对于大多数常见的连续数值问题是合适的。对于自动编码器而言，它可以帮助我们最小化输入和重构之间的平方差，从而促使解码器学习到有效的低维表示。

卷积神经网络

使用 CrossEntropyLoss 函数，通常用来解决多分类问题。

交叉熵损失函数（CrossEntropyLoss）是用于解决分类问题的一种常见损失函数。它通常与softmax激活函数一起使用，用于衡量模型输出的概率分布与真实标签之间的差异。

交叉熵损失函数的定义基于信息论中的概念，它衡量两个概率分布之间的相似性。在分类问题中，我们希望模型的输出概率分布能够接近真实标签的分布。

优化器

torch.optim.SGD 是一种基础的随机梯度下降算法，它对每个参数都使用相同的学习率进行优化。在训练过程中，SGD 算法可以通过学习率调整、动量等技巧进行改进，但其对于参数更新的速度和方向控制较为简单，容易陷入局部最优解。

torch.optim.Adam 是一种基于自适应学习率的优化算法，能够自适应地调整每个参数的学习率，从而更好地适应不同的梯度情况。相比于 SGD 算法，Adam 算法通常能够更快地收敛，在处理大规模数据和复杂模型时，也往往能够取得更好的效果。

因此，在选择使用 torch.optim.SGD 还是 torch.optim.Adam 时，可以参考以下几点建议：

数据规模和模型复杂度：当数据规模较大或模型较为复杂时，可以考虑使用 Adam 算法，因为它能够自适应地调整每个参数的学习率，并能够更好地适应不同的梯度情况。
训练速度和效果：当训练速度和效果都比较重要时，可以根据实验结果选择合适的优化算法。通常情况下，SGD 算法的速度相对较快，但容易陷入局部最优解，而 Adam 算法的效果较好，但相对较慢。
调整学习率的需求：SGD 算法需要手动调整学习率，而 Adam 算法通常不需要手动调整学习率，可以根据实验需要选择是否需要手动调整学习率。

综上所述，当数据规模较大、模型较为复杂或需要较好的训练效果时，可以考虑使用torch.optim.Adam 算法；而当数据规模较小、模型较简单或需要较快的训练速度时，可以考虑使用 torch.optim.SGD 算法。在实际使用时，也可以尝试使用不同的优化算法进行比较，根据实验结果选择最合适的算法。

卷积层参数

python

class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Conv2d(1, 32, 3, padding=1)
        self.conv2 = nn.Conv2d(32, 64, 3, padding=1)
        self.fc1 = nn.Linear(64 * 8 * 8, 128)
        self.fc2 = nn.Linear(128, 10)
        self.relu = nn.ReLU()
        self.pool = nn.MaxPool2d(2, 2)

    def forward(self, x):
        x = self.pool(self.relu(self.conv1(x)))
        x = self.pool(self.relu(self.conv2(x)))
        x = x.view(-1, 64 * 8 * 8)
        x = self.relu(self.fc1(x))
        x = self.fc2(x)
        return x

self.fc1 = nn.Linear(64 * 8 * 8, 128)中的参数是 64 * 8 * 8（依次是通道，宽和高）

在给定的代码中，self.fc1 = nn.Linear(64 * 8 * 8, 128)中的参数(64 * 8 * 8)表示前一层的输出特征图的大小。

在这个例子中，经过两个卷积层和池化层后，特征图的尺寸被减小到原始输入的1/4，即8 * 8。而在第二个卷积层之后，有64个特征图。

因此，64 * 8 * 8表示在第二个卷积层之后，展平的特征图的总大小为64 * 8 * 8。这个值作为输入传递给全连接层(nn.Linear)，并且输出维度被设置为128。

总而言之，self.fc1 = nn.Linear(64 * 8 * 8, 128)中的参数(64 * 8 * 8)是根据模型结构和输入数据的大小推导出来的，以确保正确的连接和尺寸匹配。

64 * 8 * 8这三个数字各代表什么

在这个上下文中，64 * 8 * 8 中的三个数字代表以下内容：

64：表示第二个卷积层的输出通道数。在该模型中，第一个卷积层输出的特征图通道数为32，而第二个卷积层输出的特征图通道数为64。
8：表示经过卷积和池化操作后，特征图的空间尺寸（宽度和高度）被缩减为8。在给定的代码中，通过使用大小为3的卷积核（padding=1）和大小为2的最大池化层（stride=2），每个池化层将特征图的空间尺寸减小一半。
8：表示经过卷积和池化操作后，特征图的空间尺寸（宽度和高度）被缩减为8。在这个模型中，经过两个池化层，每个池化层将特征图的空间尺寸减小一半，所以初始的输入特征图的尺寸应为 8 * 8。

综上所述，64 * 8 * 8 表示第二个卷积层后展平的特征图的总大小，其中64是特征图的通道数，8 * 8 是特征图的空间尺寸。这个值被用作第一个全连接层的输入尺寸。

池化层

self.pool = nn.MaxPool2d(2, 2) 将输入的特征图进行2倍下采样，通过将每个2x2的窗口内的最大值保留下来，而丢弃其他值。这样可以减小特征图的空间尺寸，同时保留重要的特征信息。在给定的代码中，该最大池化层被应用于两个卷积层之后，用于进一步减小特征图的尺寸。

预测

在机器学习中，predict和predict_proba都是用于预测模型输出的函数，但它们的作用略有不同。

predict函数主要用于分类任务，它接收输入数据并返回一个预测的类别，例如二元分类任务中的0或1，或多元分类任务中的类别编号。predict函数基于模型输出的类别概率进行决策，通常使用的是softmax函数。

predict_proba函数也用于分类任务，但与predict不同的是，它返回的是每个类别的概率估计值，而不是一个类别标签。这些概率值可以用于评估模型的不确定性，并帮助我们更好地理解模型的输出。predict_proba函数通常在二元或多元分类任务中使用，它们也可以使用softmax函数来计算类别概率。

需要注意的是，predict_proba函数的输出结果是一个概率向量，其中每个元素对应一个类别的概率值，这些概率值的总和为1。在一些应用场景中，我们可能只关心某个类别是否发生，而不是它的概率值，这时候可以使用predict函数，将概率估计值转化为类别标签。

生成数据

数据之间划分

np.linspace(0, 10, 100)

0 - 10 之间划分为100份

按指定步长划分

np.arange(0,2*np.pi,0.1)

定义模型

在最后一层的全连接层中不使用激活函数是常见的做法。

在分类问题中，通常将最后一层的全连接层输出作为模型的原始预测值，然后再应用 softmax 函数或其他概率分布函数来生成最终的类别预测。这样的做法可以保持输出的线性范围，方便进行概率计算。

因此，在这种情况下，self.fc2 层的输出直接作为模型的原始预测值，而没有应用额外的激活函数。

E ​

简单的线性回归 ​

分析 ​

.reshape 有什么作用 ​

为什么TrainDataHeight 需要Reshape,而TrainDataWeight不用 ​

中文画图乱码 ​

重写配置文件 ​

数据归一化 ​

meshgrid ​

重塑数组结构 ​

损失函数选择 ​

应用 ​

自动编码解码器 ​

卷积神经网络 ​

优化器 ​

卷积层参数 ​

池化层 ​

预测 ​

生成数据 ​

数据之间划分 ​

按指定步长划分 ​

定义模型 ​

E

简单的线性回归

分析

.reshape 有什么作用

为什么TrainDataHeight 需要Reshape,而TrainDataWeight不用

中文画图乱码

重写配置文件

数据归一化

meshgrid

重塑数组结构

损失函数选择

应用

自动编码解码器

卷积神经网络

优化器

卷积层参数

池化层

预测

生成数据

数据之间划分

按指定步长划分

定义模型